内容主要来自 Coursera 课程 Big Data Graph Analytics,在这对 Cypher 语句做个整理,方便查阅。包括基本语句、以及路径分析、链接分析样例。
Neo4j 使用 Cypher 查询图形数据,Cypher 是描述性的图形查询语言,语法简单功能强大,由于 Neo4j 在图形数据库家族中处于绝对领先的地位,拥有众多的用户基数,Cypher 成为图形查询语言的事实上的标准。
和 SQL 很相似,Cypher 语言的关键字不区分大小写,但是属性值,标签,关系类型和变量是区分大小写的。
看一下基本的概念
变量(Variable)
变量用于对搜索模式的部分进行命名,并在同一个查询中引用,在小括号()中命名变量,变量名是区分大小写的,示例代码创建了两个变量:n 和 b,通过 return 子句返回变量 b;12MATCH (n)-->(b)RETURN b访问属性(Property)
在 Cypher 查询中,通过点来访问属性,格式是:Variable.PropertyKey,通过 id 函数来访问实体的 ID,格式是 id(Variable)。123match (n)-->(b)where id(n)=5 and b.age=18return b;节点(Node)
节点模式的构成:(Variable:Lable1 {Key1:Value1,Key2,Value2})
每个节点都有一个整数 ID,在创建新的节点时,Neo4j 自动为节点设置 ID 值,在整个数据库中,节点的 ID 值是递增和唯一的。
下面的 Cypher 查询创建一个节点,标签是 Person,具有两个属性 name 和 born,通过 RETURN 子句,返回新建的节点:1create (n:Person { name: 'Tom Hanks', born: 1956 }) return n;匹配(Match)
通过match子句查询数据库,match子句用于指定搜索的模式(Pattern),where子句为match模式增加谓词(Predicate),用于对Pattern进行约束;1match(n) return n;关系(Relation)
关系的构成:StartNode - [Variable:RelationshipType {Key1:Value1, Key2:Value2}] -> EndNode
创建关系时,必须指定关系类型1234MATCH (a:Person),(b:Movie)WHERE a.name = 'Robert Zemeckis' AND b.title = 'Forrest Gump'CREATE (a)-[r:DIRECTED]->(b)RETURN r;
本篇数据集:
链接: http://pan.baidu.com/s/1dEHWQch
密码: 00v4
Create and Delete
建图要求
创建完整的 graph
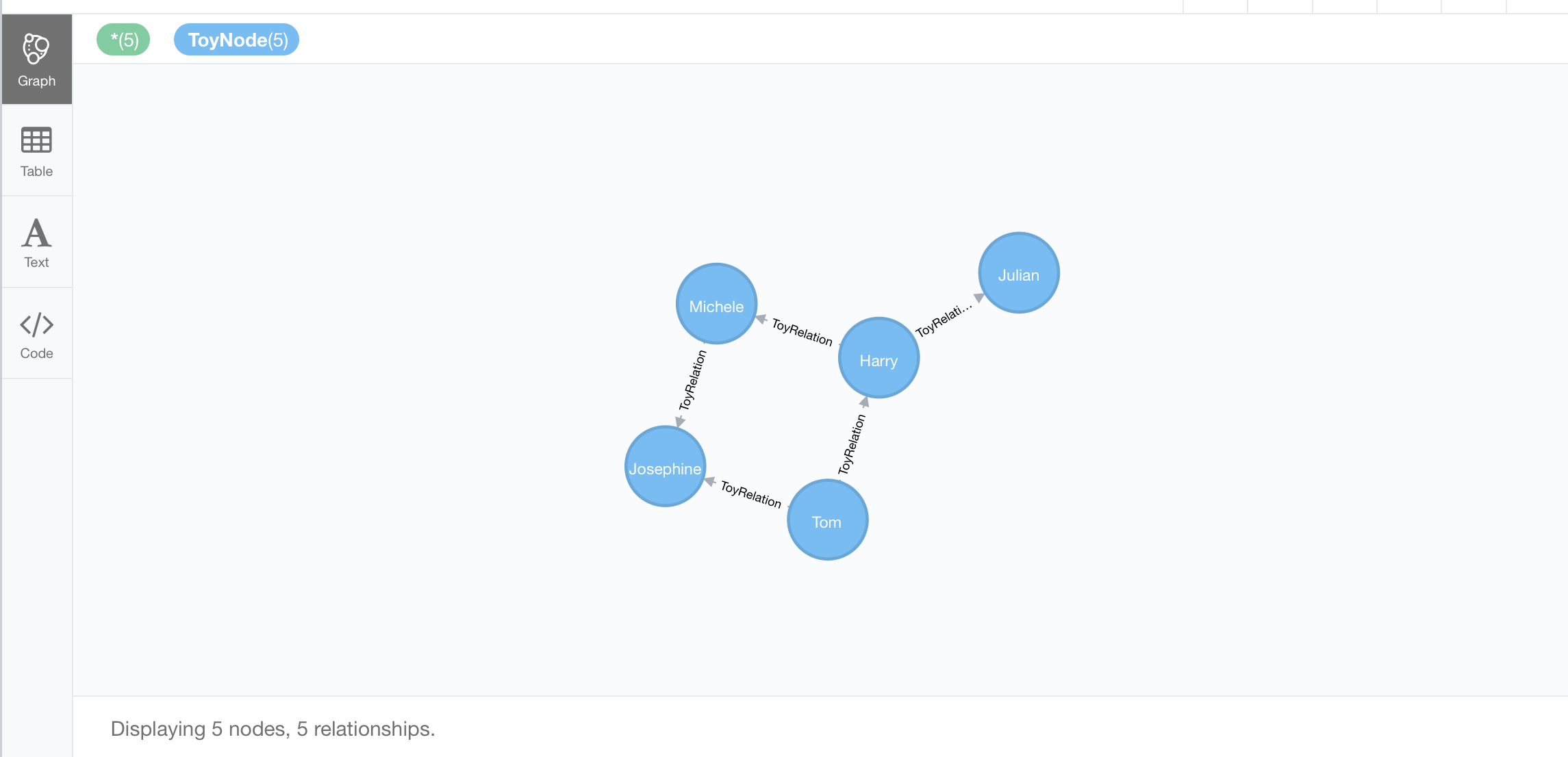
ToyNode is a node type and ToyRelation is an edge type. ToyNode can have properties, so can ToyRelation.
//View the resulting graph
//Delete all nodes and edges
//Delete all nodes which have no edges
//Delete only ToyNode nodes which have no edges
//Delete all edges
//Delete only ToyRelation edges
//Selecting an existing single ToyNode node
Adding or Modify
Merge 子句的作用:当模式(Pattern)存在时,匹配该模式;当模式不存在时,创建新的模式,功能是 match 子句和 create 的组合。在 merge 子句之后,可以显式指定 on create 和 on match 子句,用于修改绑定的节点或关系的属性。
通过 merge 子句,可以指定图形中必须存在一个节点,该节点必须具有特定的标签,属性等,如果不存在,那么 merge 子句将创建相应的节点。
//Adding a Node Correctly
First find a node you wanna add to, then add the node.
//Adding a Node Incorrectly
//Correct your mistake by deleting the bad nodes and edge
//Modify a Node’s Information
Import
//One way to “clean the slate” in Neo4j before importing (run both lines):
//Script to Import Data Set: test.csv (simple road network)
//[NOTE: replace any spaces in your path with %20, “percent twenty” ]
//Script to import global terrorist data
When you are loading CSVs you get an error like “Couldn’t load the external resource at: file: […]”, put your csv file in the right path like /Users/shuang/Documents/Neo4j/default.graphdb/import/, the problem will be solved.
Basic Graph Operations
//Counting the number of nodes
//Counting the number of edges
//Finding leaf nodes:
Leaf node: the node which have no outgoing edges
//Finding root nodes:
Root node: the node which have no incoming edges
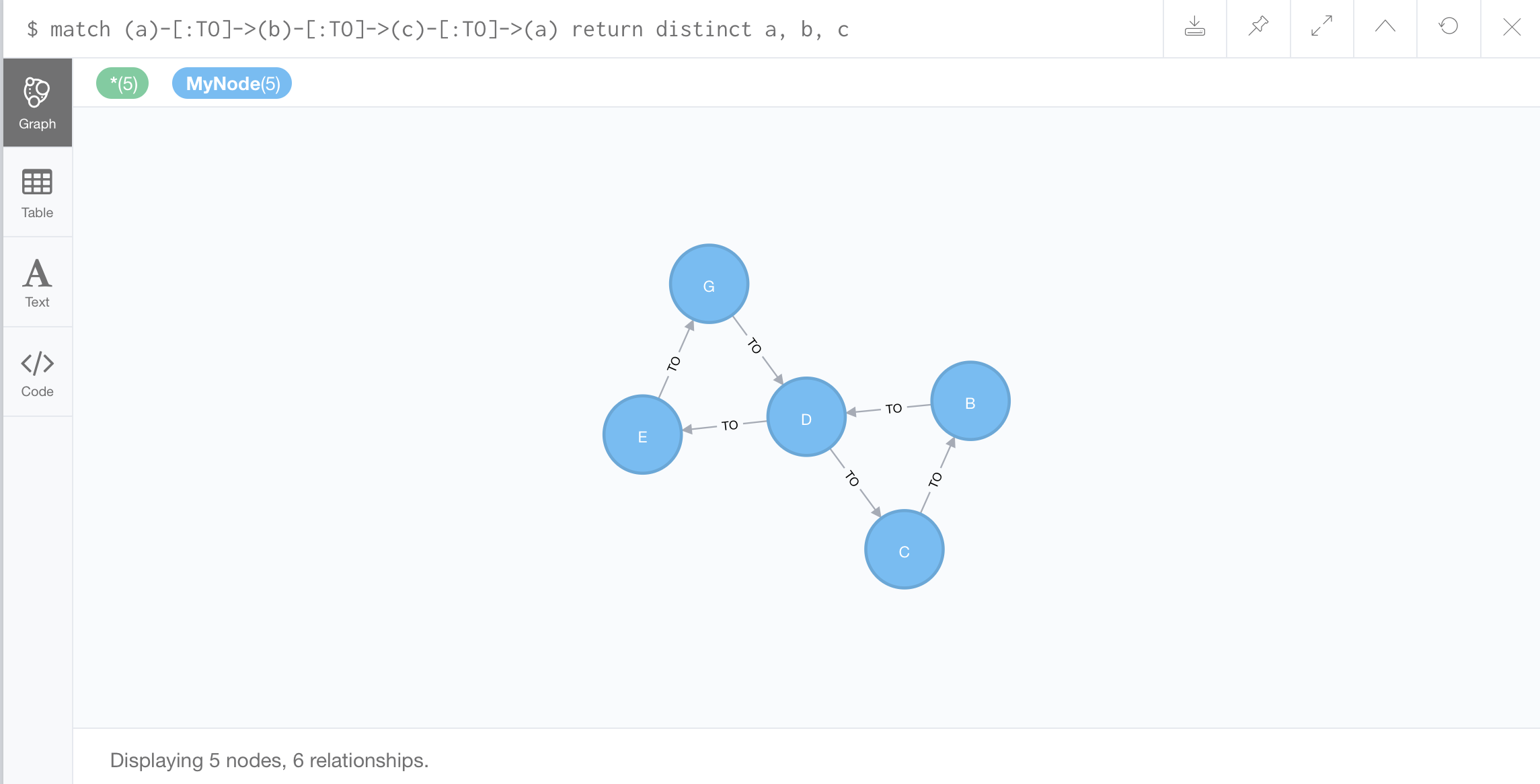
//Finding triangles:
Triangle: a three cycle, consisting of three nodes and three edges where the beginning and end node are the same
//Finding 2nd neighbors of D:
2nd neighbor: two nodes away from D
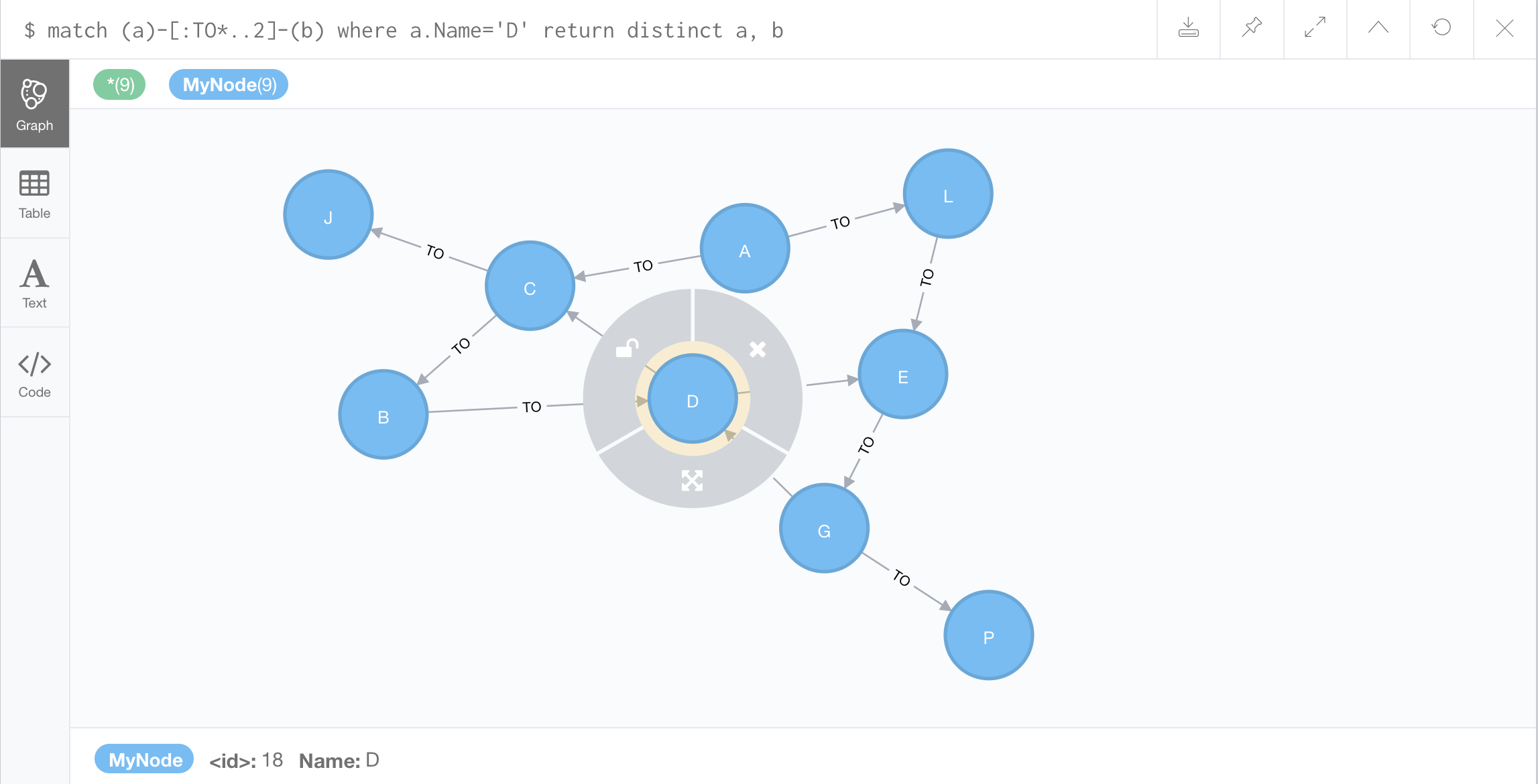
Some nodes appear to be only one node away from the node D but we can get to those nodes indirectly through another node, which means that they’re not only a first neighbor but they’re also a second neighbor.
//Finding the types of a node:
//Finding the label of an edge:
//Finding all properties of a node:
//Finding loops:
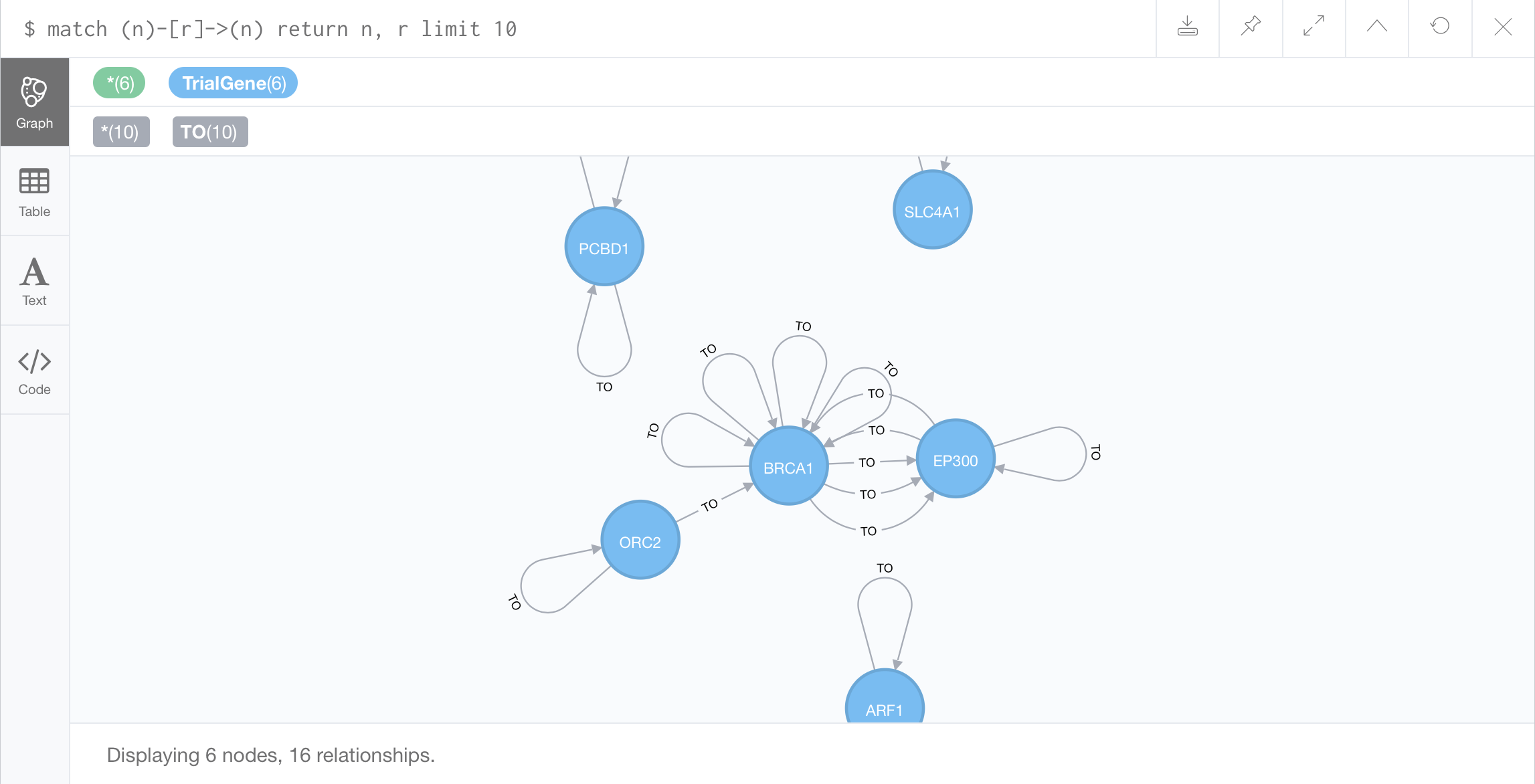
//Finding multigraphs:
Multigraph: any two nodes which have two or more edges between them
remember to apply a constraint in which the edges must be different for the same pairs of nodes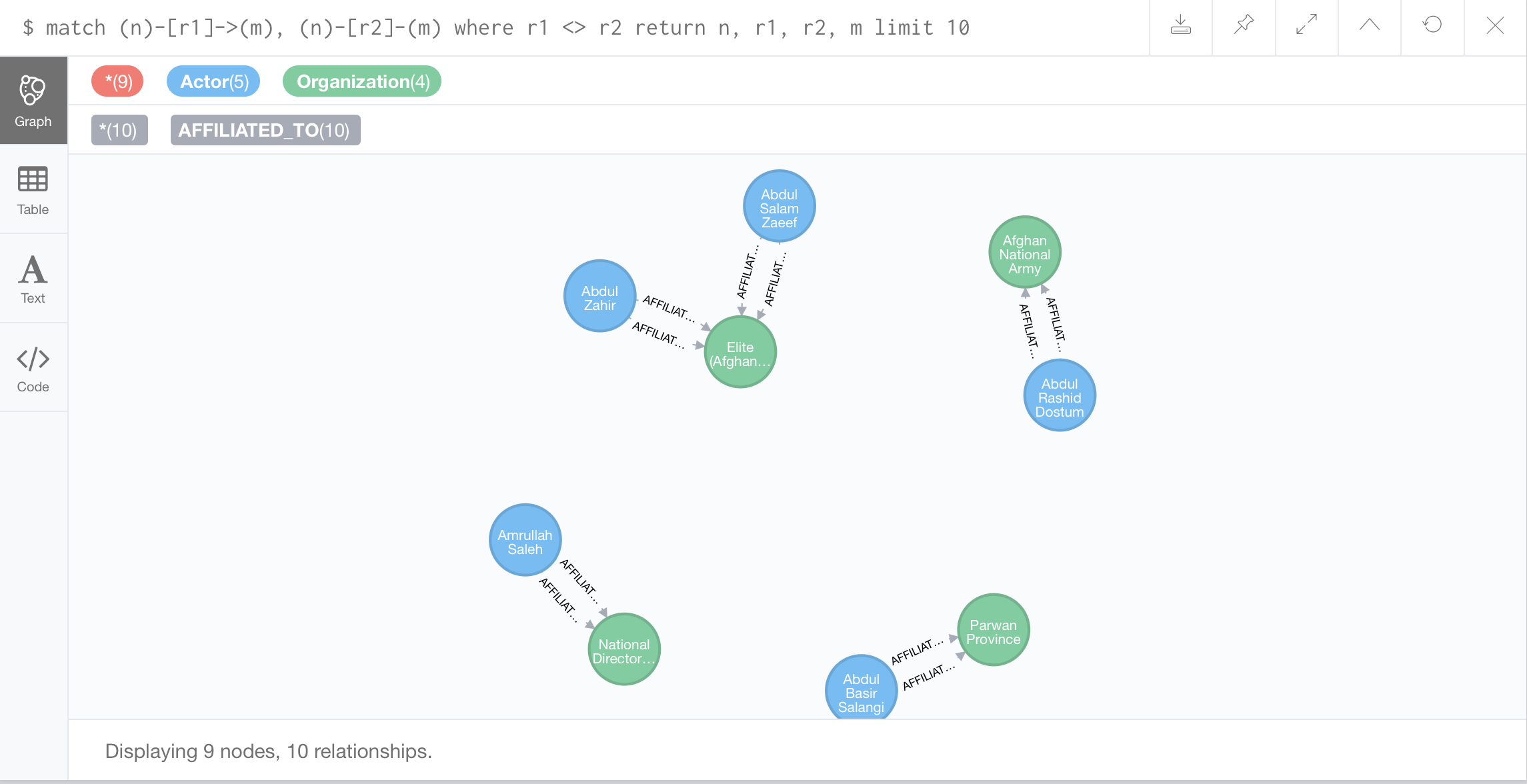
//Finding the induced subgraph given a set of nodes:
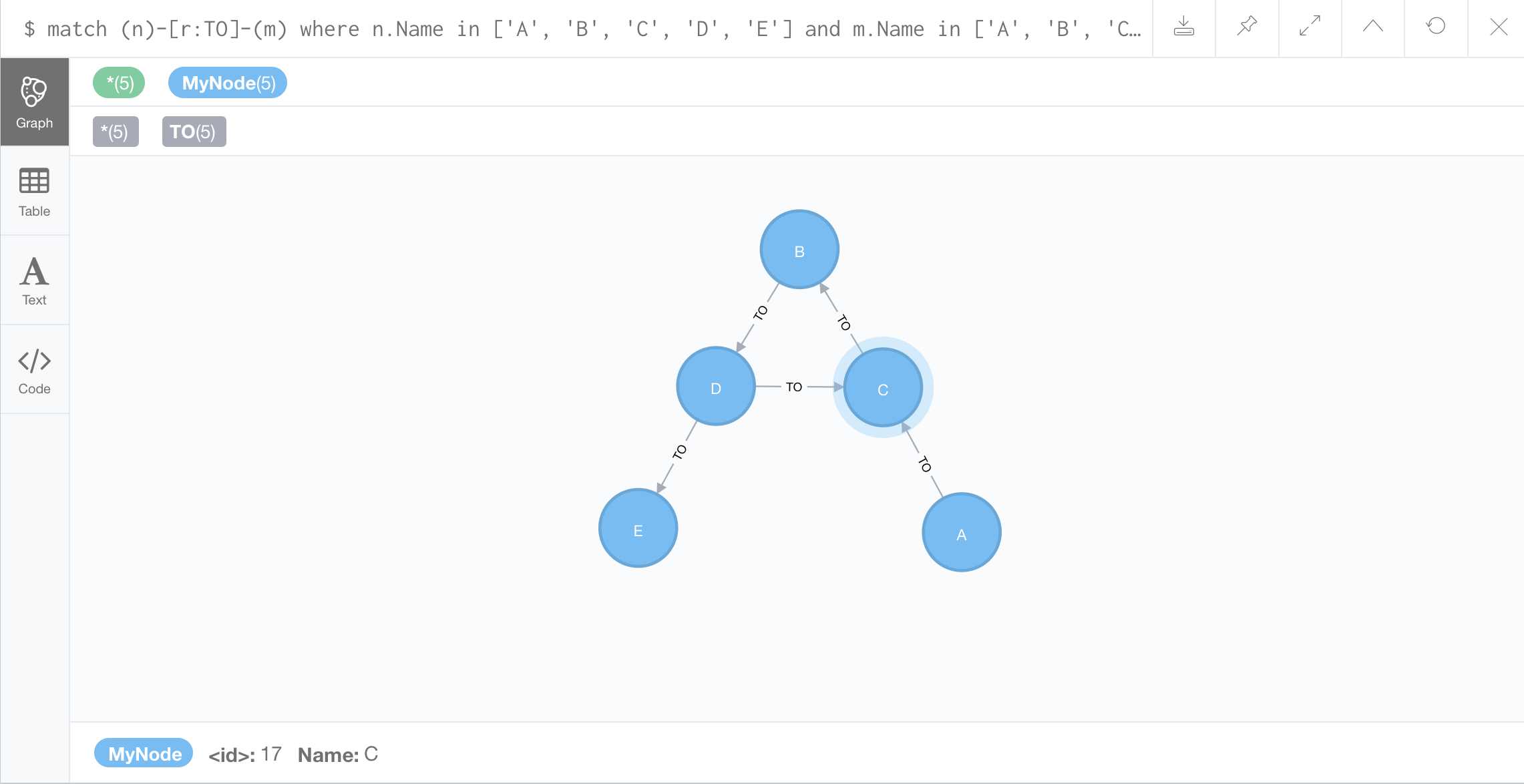
Path Analytics
//Viewing the graph
//Finding paths between specific nodes:
Use the match command to match p which is a variable we’re using to represent our path, = node a, going through an edge to node c. There’s something slightly different about this edge, and that is that we’re using a star to represent an arbitrary number of edges in sequence between a and c, and we’ll be returning all of those edges that are necessary to complete the path. And in this case we only want to return a single path.
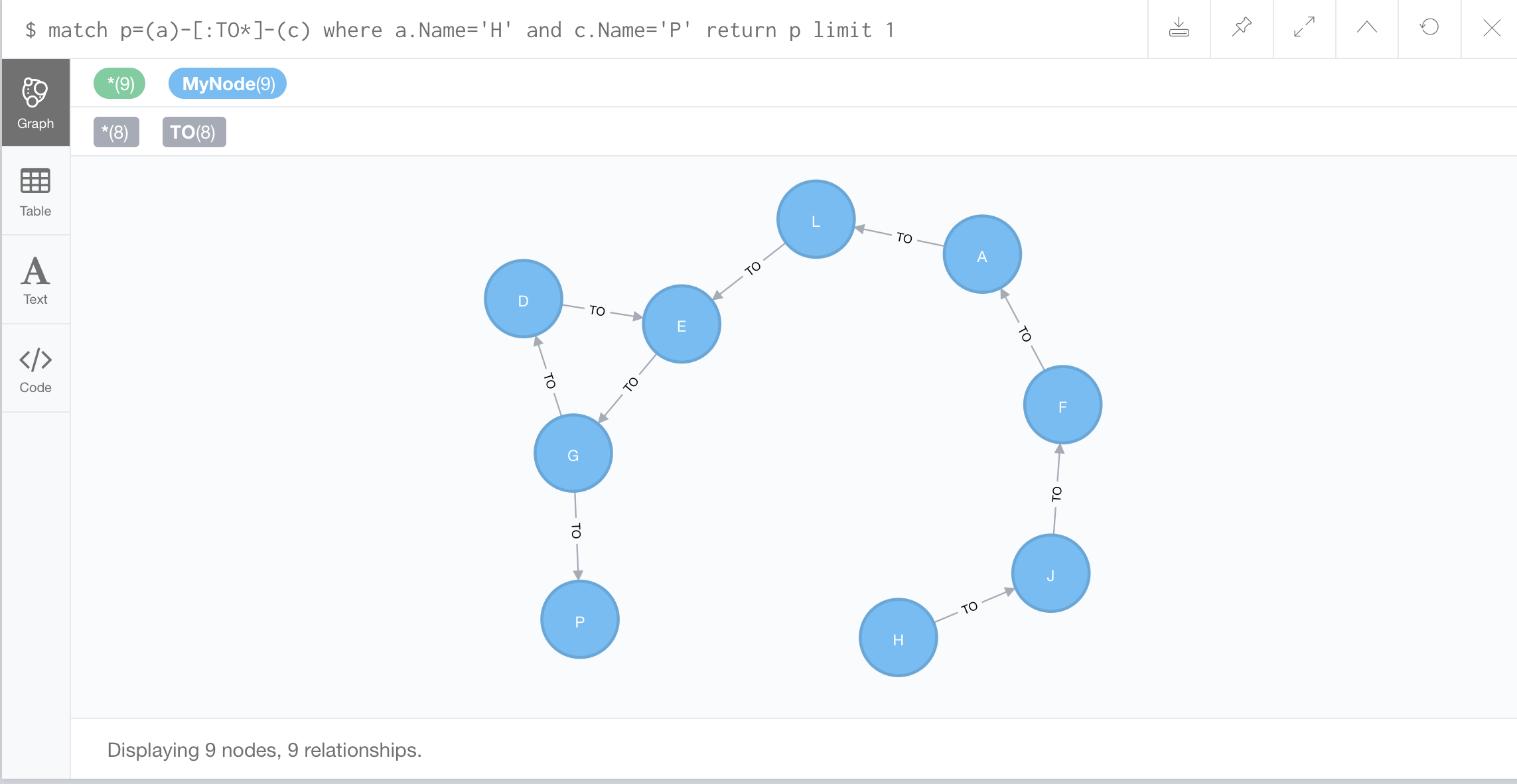
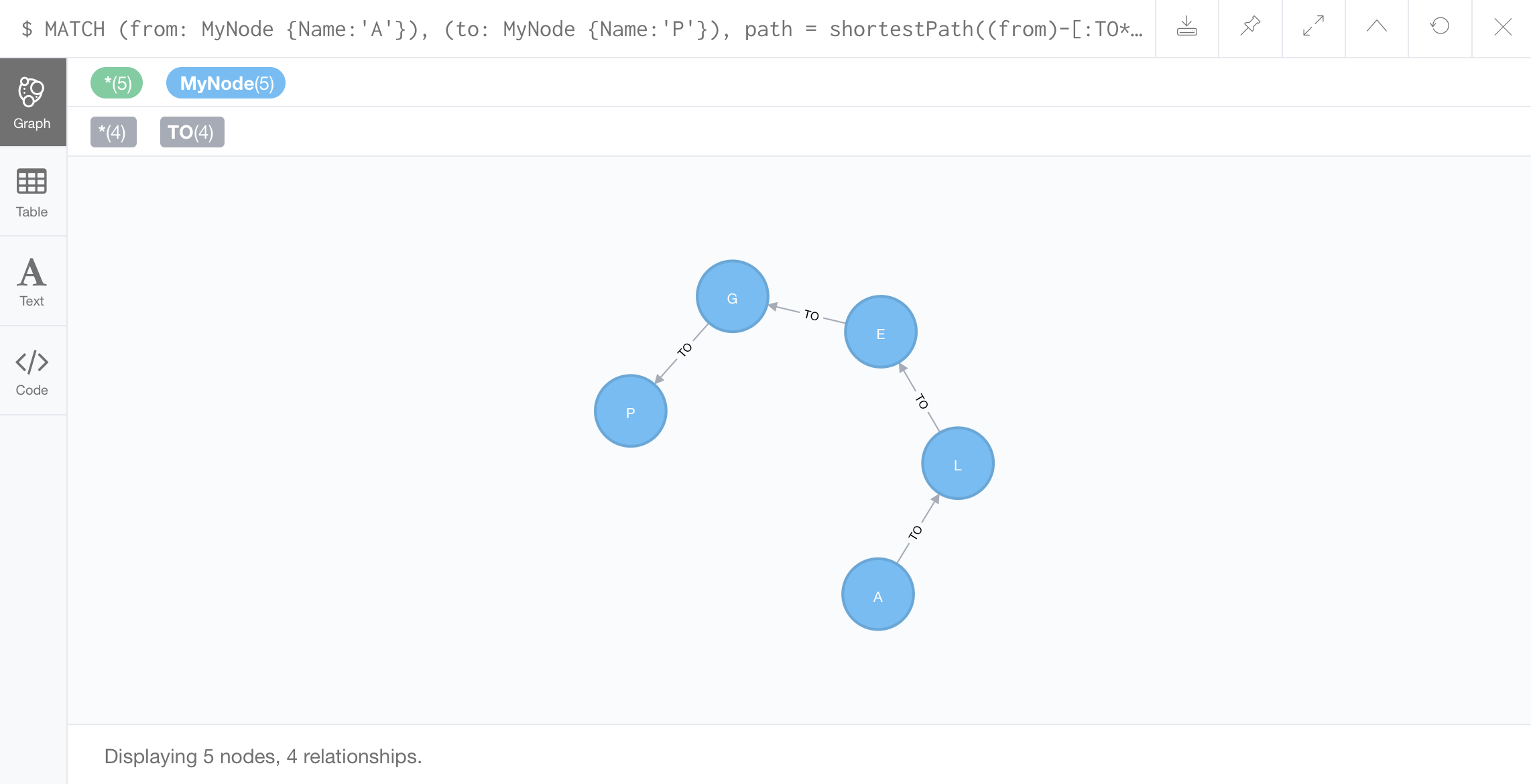
*Your results might not be the same as the video hands-on demo. If not, try the following query and it should return the shortest path between nodes H and P:
//Finding the length between specific nodes:
//Finding a shortest path between specific nodes:
Use a built-in command shortestPath
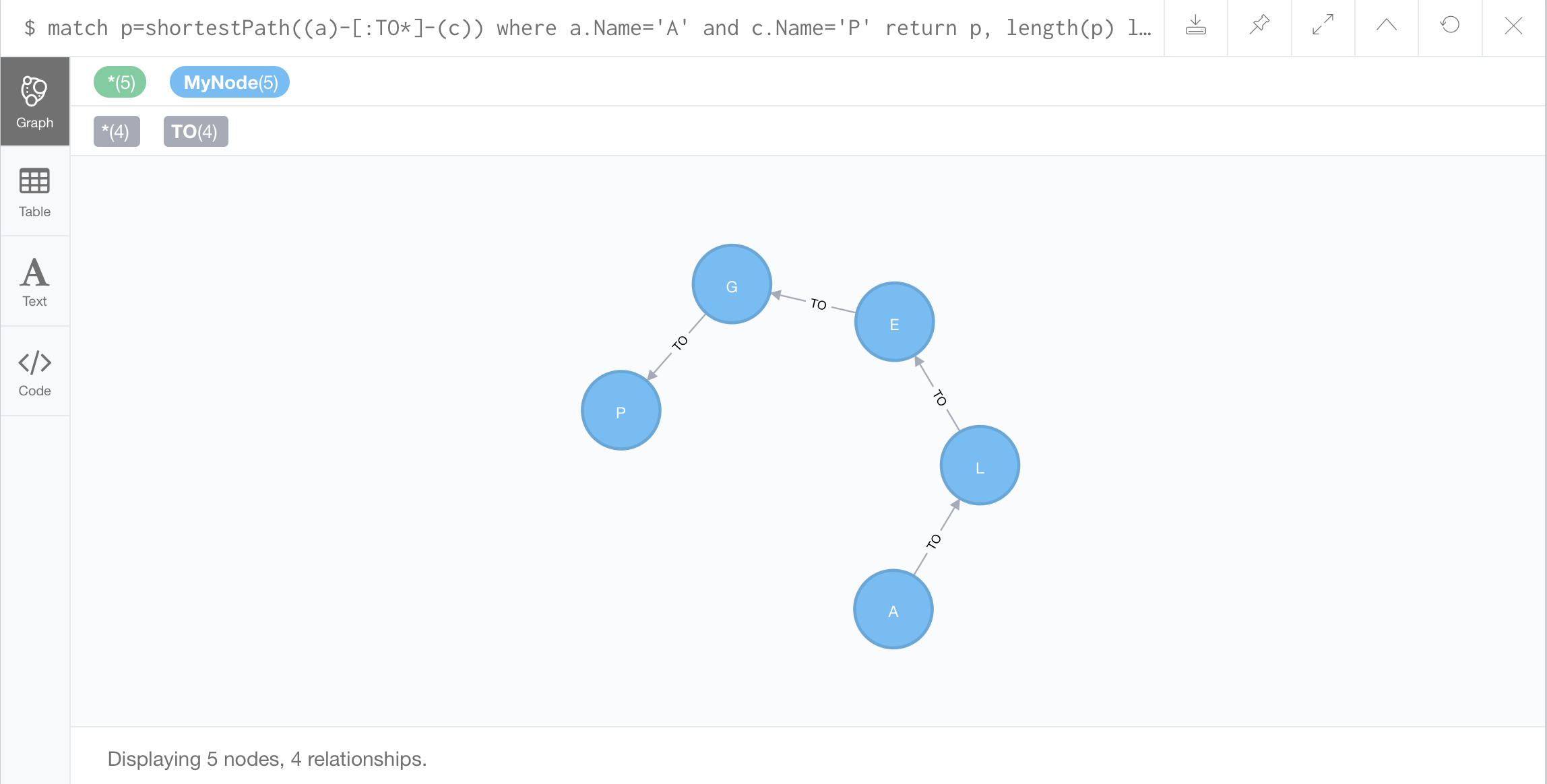
//All Shortest Paths:
Use a built-in command allShortestPaths
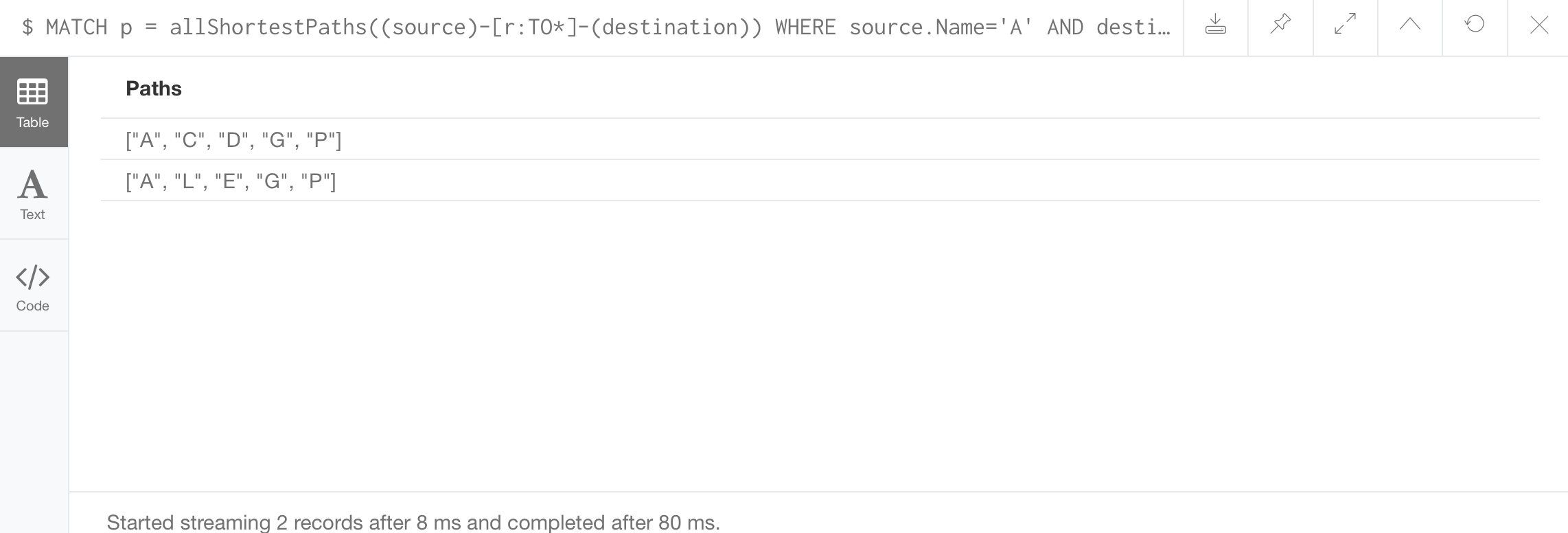
//All Shortest Paths with Path Conditions:
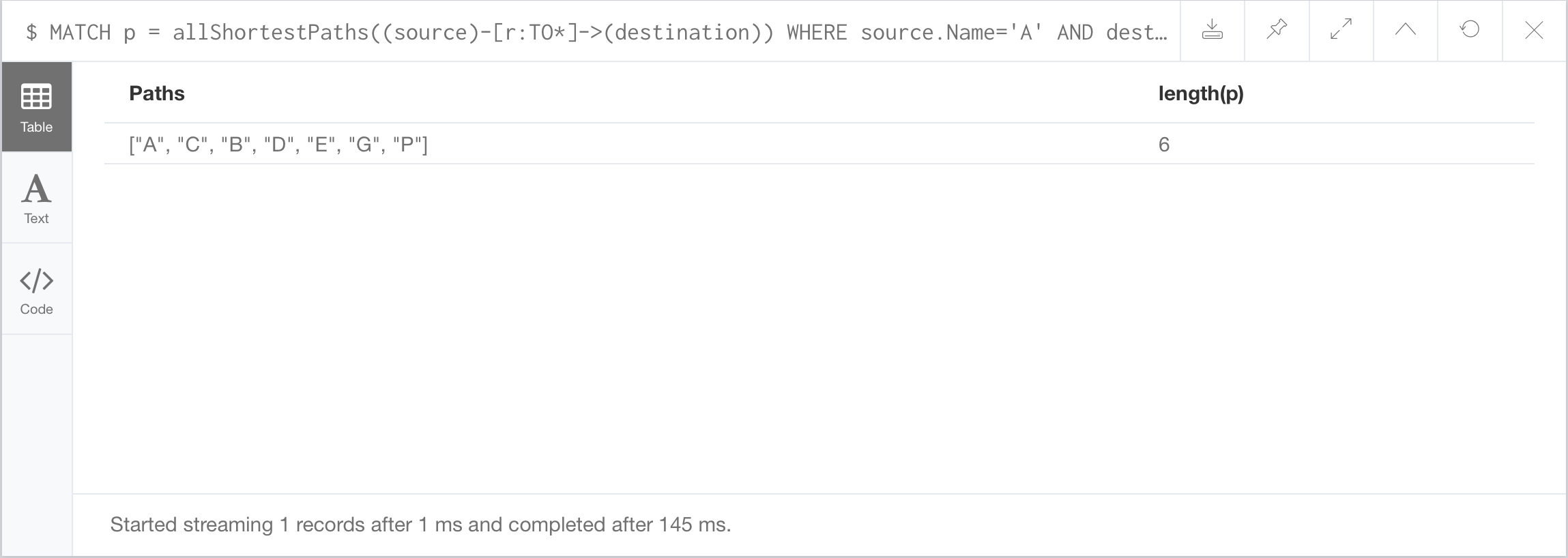
//Diameter of the graph:
Diameter: the longest shortest path between two nodes in the graph
Returned in the form of an array. We’re using a new term, extract, which is based on the following. Assuming we have matched our path p, we want to identify all of the nodes in p and extract their names. And we’ll return these names as a listing, which we’ll call the variable paths. If there’s more than one shortest path, we’ll get multiple listings of node names.
//Extracting and computing with node and properties:
Returned as the variable pathLength.
Reduce line begins by setting a variable s equal to 0. And then define a variable e, which represents the set of relationships in a path that’s returned,
or in other words, the edges. And we pass that into this variable s, and add to it, the value of the distance that we’ve assigned to that edge.
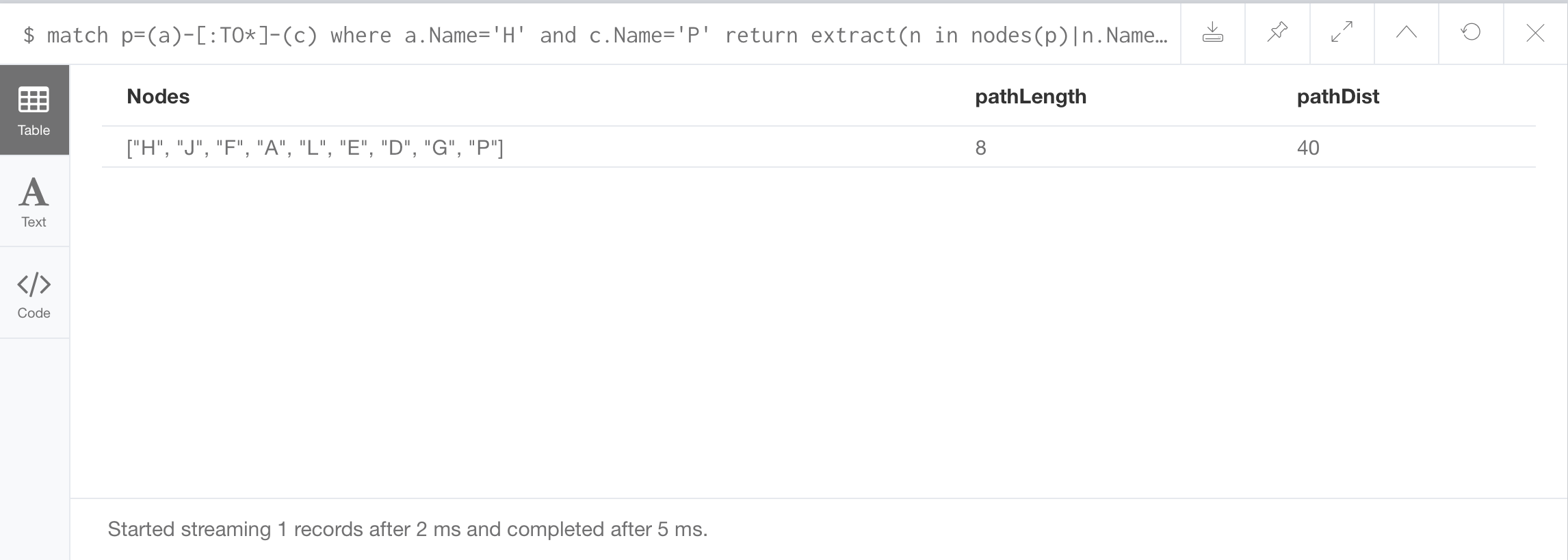
The path itself, as we know, begins in H and ends in P. And it has a pathLength of 8, but it has a pathDist of 40.
So we could interpret this to mean that even though there are 7 towns between the source town and the destination town, or a pathLength of 8,
the actual distance in miles would be a value of 40.
//Dijkstra’s algorithm for a specific target node:
This is not the path in our network with the least weights. It is the weight of the shortest path based on numbers of hops.
//Dijkstra’s algorithm SSSP:
What we’ve calculated is the shortest hop path with the weights added, the sum of the weights of the edges in that path. This is not the least weight path of the entire network.
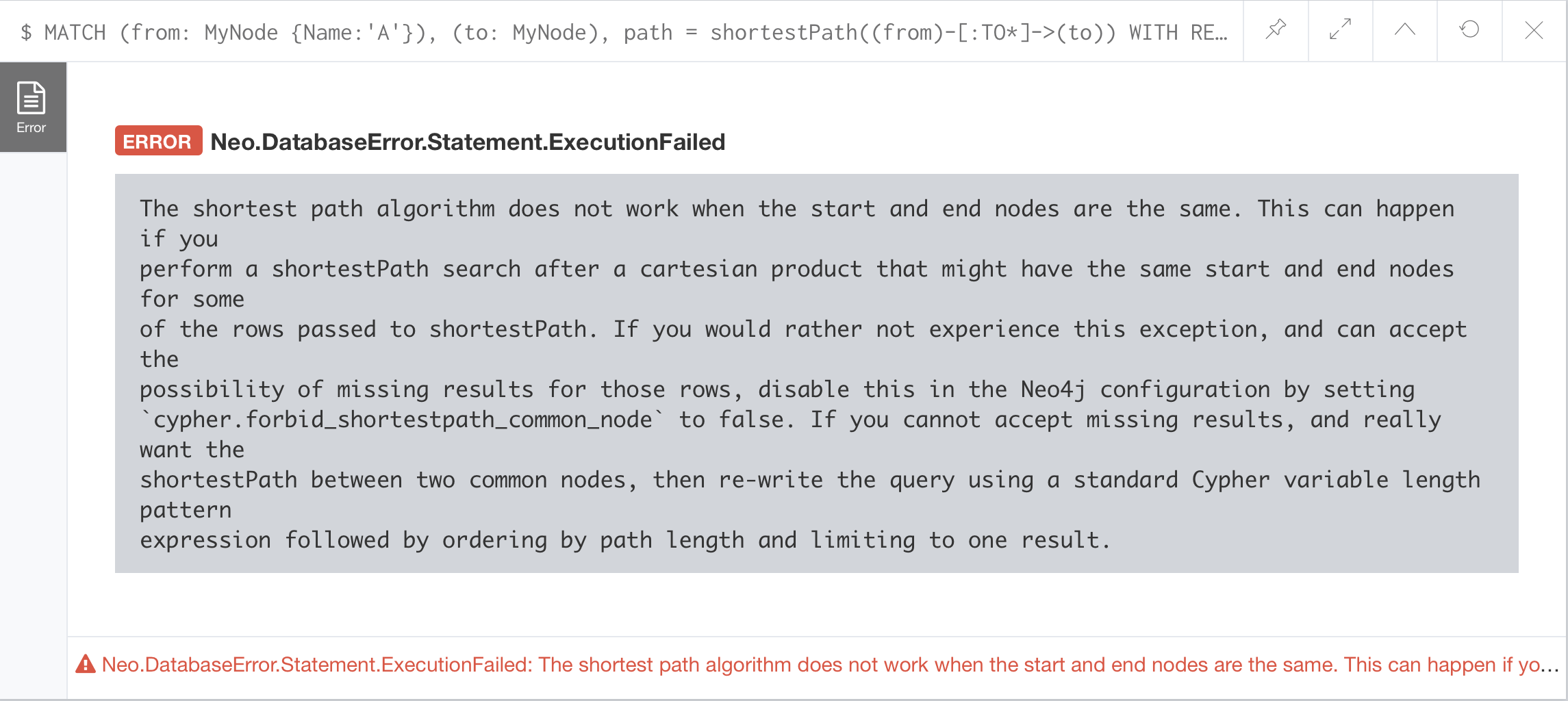
Problem not solved. Refer to allshortestPaths error start/end nodes the same with cypher.forbid_shortestpath_common_node=false
//Graph not containing a selected node:
//Shortest path over a Graph not containing a selected node:
//Graph not containing the immediate neighborhood of a specified node:
Remember to take leaf and root node into account.
The result for first statement.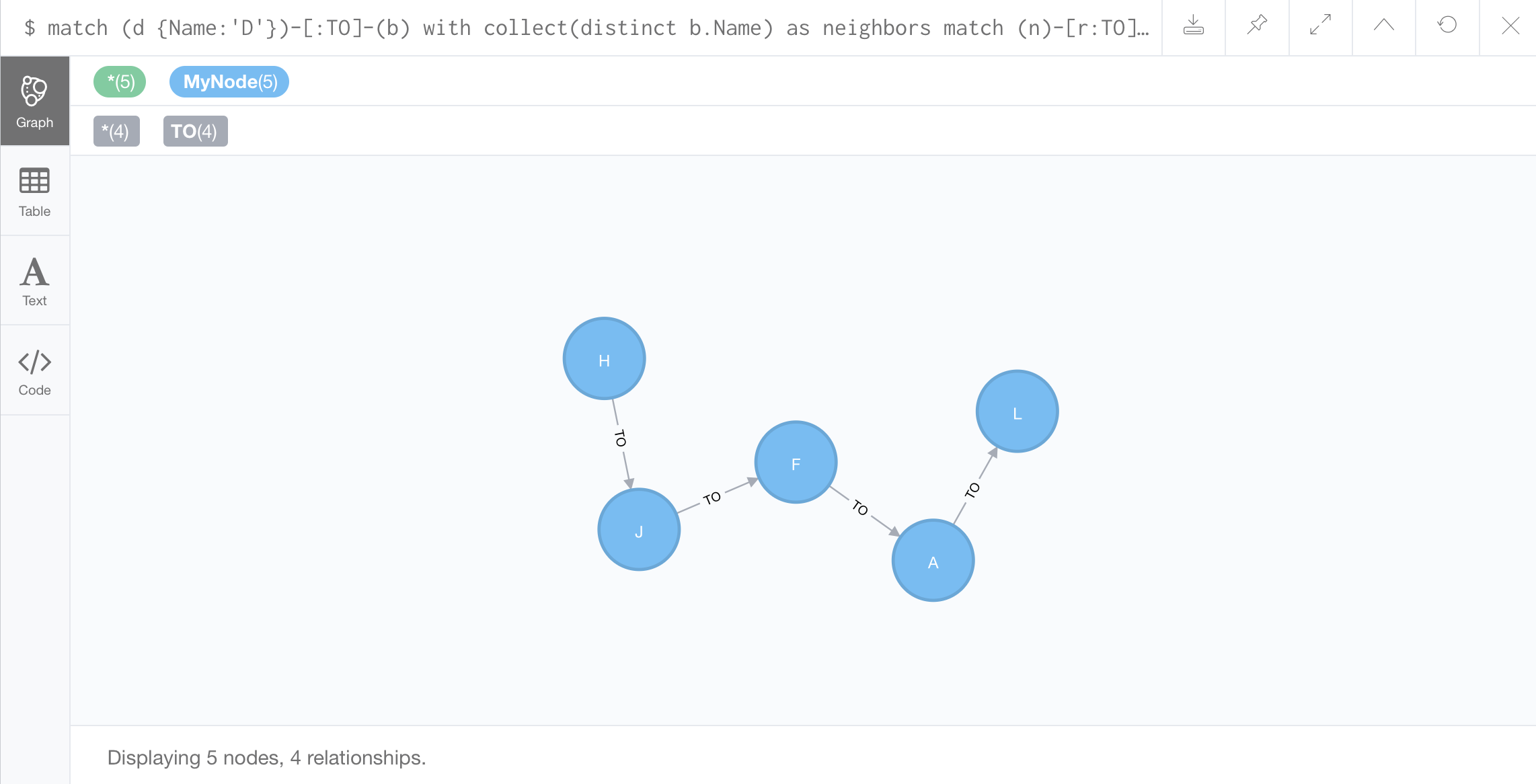
//Graph not containing a selected neighborhood:
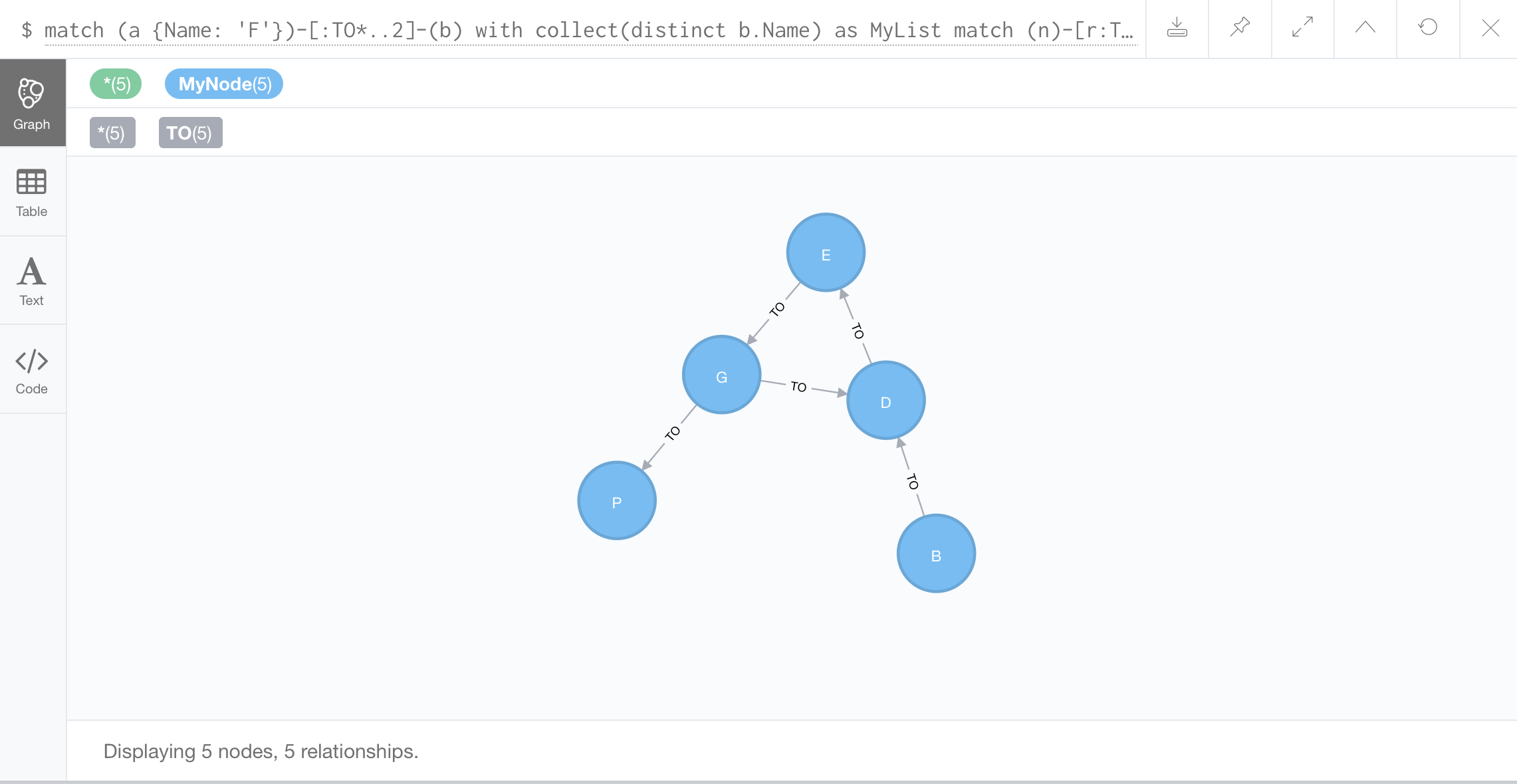
Connectivity Analytics
Connectivity analytics in terms of network robustness. In other words, a measure of how resistant a graph network is to being disconnected
Two ways of connectivity analytics: One computed the eigenvalues, and the second computed the degree distribution. For these examples, we’re going to use the second one, degree distributions.
//Viewing the graph
// Find the outdegree of all nodes
// Find the indegree of all nodes
// Find the degree of all nodes
// Find degree histogram of the graph
//Save the degree of the node as a new node property
// Construct the Adjacency Matrix of the graph
Philosophical issue:
Every database will allow you some analytical computation and the remainder of the analytical computations must be done outside of the database. However, it is always a judicious idea to get the database to achieve an intermediate result formatted in a way that you would need for the next computation. And then, you use that intermediate result as the input to the next computation. We’ve seen that a number of computations in graph analytics start with the adjacency matrix. So we should be able to force Cypher to produce an adjacency matrix
// Construct the Normalized Laplacian Matrix of the graph
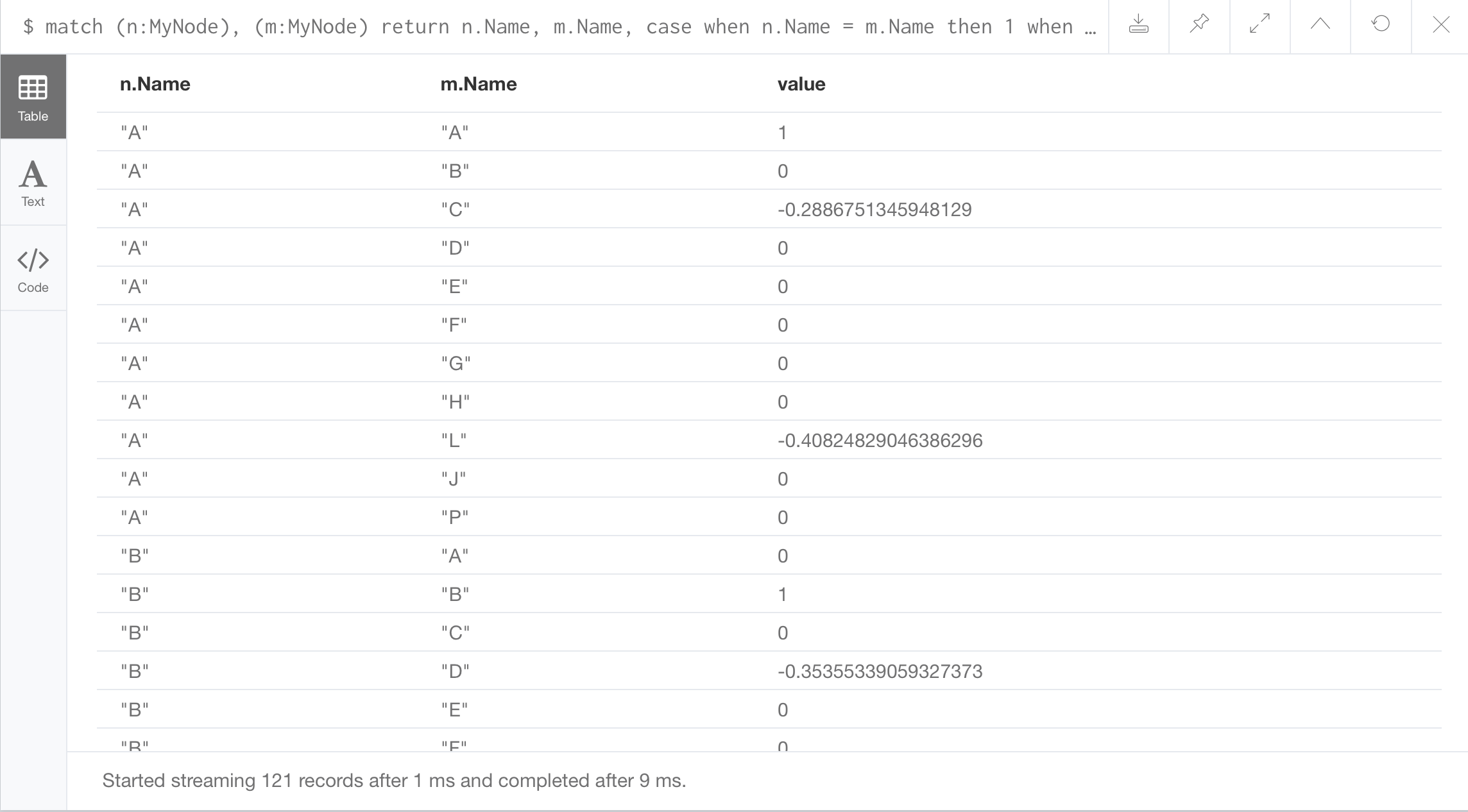
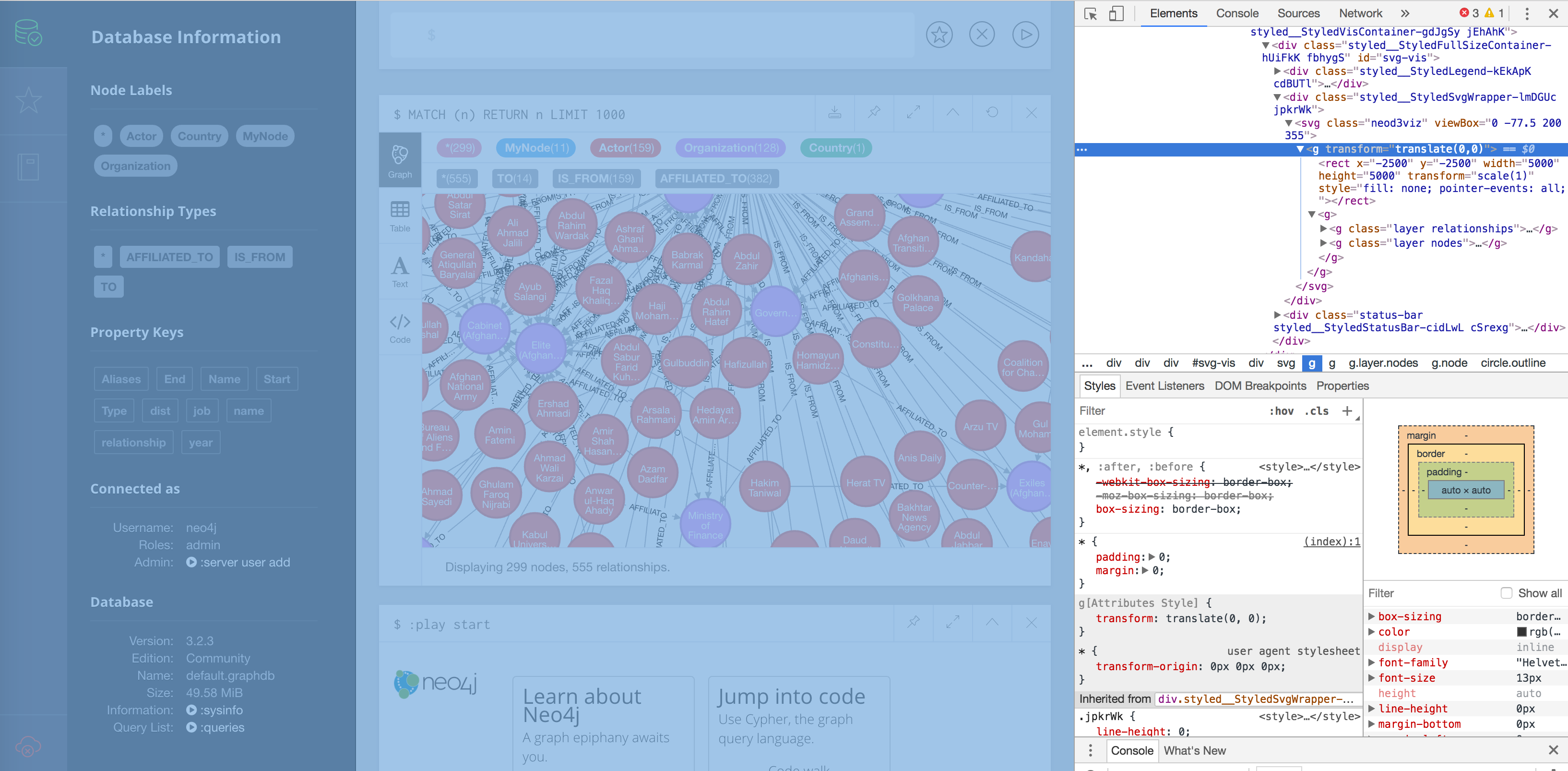
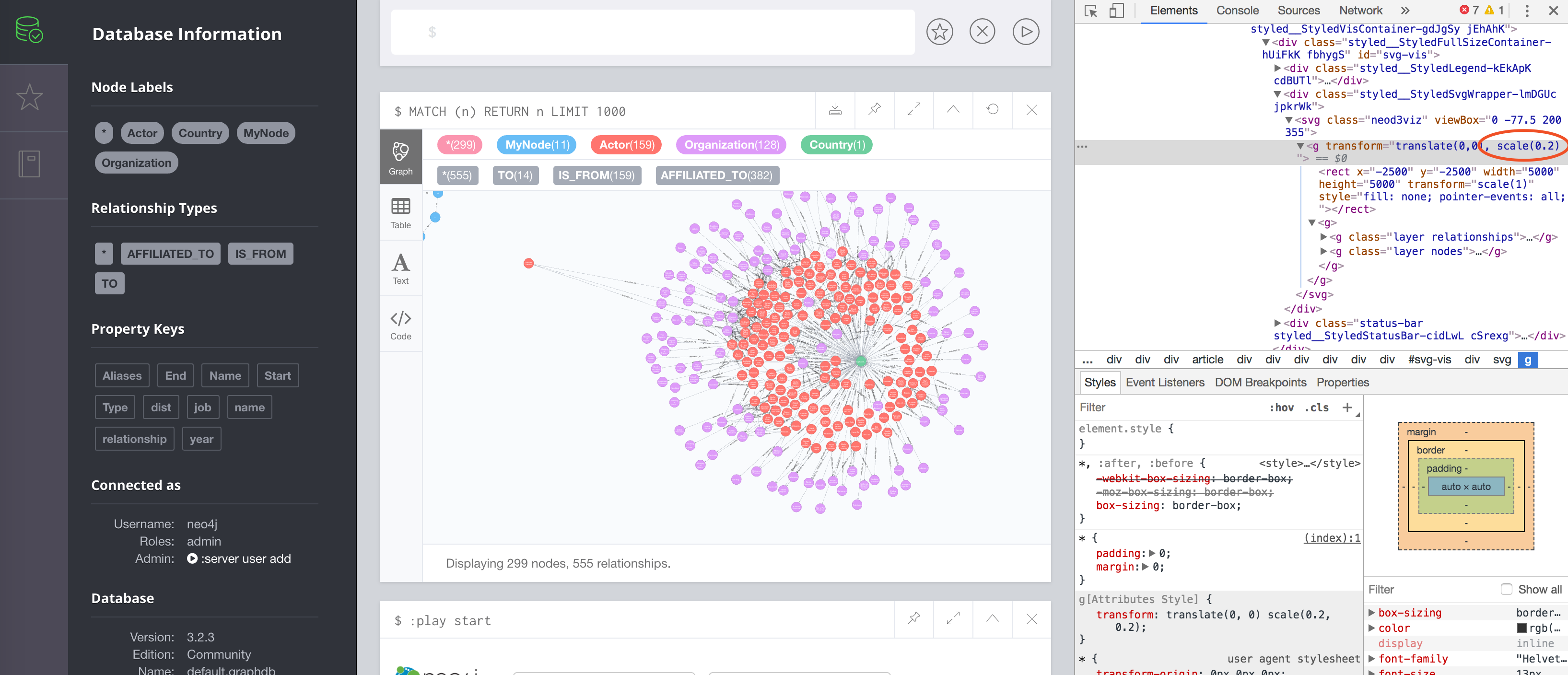
Scale View
可以调整显示区的大小,浏览器调到 inspect 模式,在 d3 代码区域添加 scale 函数,如下。
References:

